レトロゲームにおける確率論
【はじめに】(2002/07/18)
次のような質問がたまに来ます。
『攻略本には発生率1/32と書いてあるのに、32回以上やってもなかなか発生しません。簡単に発生させる良い方法はありませんか?』
おそらく質問された方は、何かしらの裏技で簡単にできるのでないかと考え、このような質問をしてきたのでしょう。しかし大方においてその様な裏技は存在しません。気合と根性で頑張るしかないのです。
これではちょっと可哀想なのでこの様なページを作ってみました。確率というのが分かっていれば、多少は頑張り甲斐があると思います。
【もっとも勘違しやすいこと】(2002/07/18)
「発生率1/32ならば32回も試行すれば一度は必ず発生するだろう」と考えている人は意外と多いのではないでしょうか? しかしそれは間違っています。
発生率1/32において32回試行し、最低でも一度発生する確率は、32回試行して全て外れた場合の余事象となるので、計算式が1-(1-1/32)^32となって、答えが約64%となります。とにかく、必ず一度発生するわけではないのです。
だから32回程度でへこたれてはなりません。64回やっても約87%なのです。とにかく頑張りましょう。
ただ、いくらやっても発生しないことがあります。その場合はゲーム内で使われている乱数に偏りがあると疑って下さい。これについては後述しますが、ひたすらやり続けることに代わりはありません。
おまけとして、発生率1/Nにおいて試行し続けた場合、最低でも一回発生する確率の近似値表を作ってみました。Nが16だったら、8回目で39.35%、16回目で63.21%、24回目で77.69%といった具合です。気休め程度に使って下さい。
| 回数 | 確率(%) |
|---|---|
| 0.5 * N | 39.35 |
| 1.0 * N | 63.21 |
| 1.5 * N | 77.69 |
| 2.0 * N | 86.47 |
| 2.5 * N | 91.79 |
| 3.0 * N | 95.02 |
| 3.5 * N | 96.98 |
| 4.0 * N | 98.17 |
※この表の値は、lim[n→∞](1-(1-1/n)^an) = 1-(1/e)^a、に由来しています。もちろんeは自然対数の底です。
【分かり易い例え】(2005/04/07)
6面体の普通のサイコロを6回振った場合、1から6の目がそれぞれ1回出現する確率が最も高い。しかし実際はなかなかそうならない。
確率なんてのはそんなもの。
【乱数の偏り】(2002/07/18)
コンピュータでは完全な乱数は扱えません。そこで計算式によって擬似的に乱数を作り上げています(疑似乱数と言う)。複雑な計算式を使えばより乱数らしくなりますが、マシンパワーが貧弱だった時代のゲームではときたま偏りがありました。疑似乱数の偏りはある意味バグですが、それに怒ってカセットを窓から放り投げるのはやめましょう。
最も広く使われていた疑似乱数の発生方法に線形合同法というのがあります。これは次のような漸化式になっています。
Xn+1 = ( a・Xn + c ) mod m
a, c は任意の数字で、mod は割り算の余りです。0 から m-1 までの範囲で乱数を発生させる事ができます。
例えば、昔のゲーム機は8bitだったので m は2の8乗で256として、割り算を使わないようにします。そして、 a = 61、 c = 5、 X0 = 3 (一般にX0のことをseedと呼びます)などとすると、
188 209 210 15 152 61 142 219 52 105……
と、いった風に乱数っぽい数列が現れます。
しかし、このままでは不完全です。奇数と偶数が交互に出現してしまっていたり、一定の周期性があるなど不具合がいくつかあります。上位ビットと下位ビットを入れ替えるなどと工夫するのですが、この辺の問題を上手く解決していないと、ゲームバランスに偏りが現れクソゲーとなってしまうのです。
疑似乱数の生成方法は他にも幾つかあります。ものによっては、乱数の立ち上がりに偏りがあるもの(M系列で初期値を失敗している時など)もあります。そういった場合、本来なら乱数を何度か空回りさせて安定させるものです。しかし、それをやっていないゲームでリセット攻勢などをかけると、なかなかお目当てのアイテムをゲットできなかったりします。そういうときは、適当にゲームを実行させて乱数を安定させるのがいいでしょう。
【よくエンカウントする】(2006/01/15)
RPGで敵に遭遇するのをエンカウントと呼びますが、エンカウント率が高い印象のゲームがあります。これは乱数の偏りだけが原因でないことがあります。これについては話が長くなるので別ページに書きました。要は確率分布の問題です。
・エンカウントについて考えてみる
【M系列乱数】(2004/08/15)
前の方で線形合同法を紹介したので、M系列乱数についても簡単に紹介したいと思います。M系列は次のような漸化式になっています。
Xn = Xn-p xor Xn-q
X は1ビットの乱数列、p と q はある法則に則った整数値(p > q)、xor は排他的論理和を意味します。乱数の周期は 2p-1 となります。あと、Xn は1ビットの値なので注意して下さい。
さて、p と q はどんな値なのかというと、次の既約多項式が因数分解できないものとなってます。
Xp + Xq + 1 = 0 (p > q > 0)
注意しなくてはいけないのは、この多項式が桁上がり等の無い1ビットの多項式だということです。例えば、 X4 + X2 + 1 = 0 は因数分解不可能に思えますが、1ビットの演算では以下の様になって因数分解できることが分かります。
(X2 + X + 1)(X2 + X + 1)
= X4 + (X3 + X3) + (X2 + X2 + X2) + (X + X) + 1
1ビットの演算なので加算が排他的論理和になる
= X4 + X2 + 1
p と q の選定は面倒くさいですが、こういうのはネット上を探せば見つかったりします。キーワードは「M系列 多項式」です。
それでは p = 3、q = 1 ということにして乱数列作ってみます。nの値がマイナスの部分は乱数列の初期値です。初期値を全て0にしてしまうと乱数列は永遠と0となってしまうので注意します。
| n | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | … |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| xn | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | … |
p = 3 なので乱数の周期は 23 - 1 = 7 となっています。
回路図っぽくすると下の図の様になります。簡単な仕組みなのでCPUなどに組み込むのも簡単です。
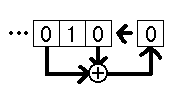
実際に使う場合は、p = 521、q = 32 ぐらいにして、乱数列から32ビット分取り出すことになります。
【ファンタシースター2の乱数は酷い】(2003/10/06)
メガドライブ版のファンタシースター2では裏技で「ビジフォン」なるものが入手できました。どこでもセーブができる便利アイテムで、こいつを入手するか否かでゲームの難易度が変わってしまう代物です。
入手方法は『シルカのレベルを10以上にして、セントラルタワーにある友達の家から盗み出させる』というものでした(シルカのレベル条項を忘れている攻略サイトが多いので注意)。
教育上非常によろしくない方法ですが、それ以上によろしくないのがシルカがビジフォンを盗み出す確率。実際にやってみた人なら分かりますが、50回ぐらいやっても成功しないなんて事があります。
実は、このゲームのプログラマー(中裕司)は1/2の確率で成功するようにプログラムしたつもりだったそうです。でも実際はとんでもなく低い確率になってます。原因はひとつ。乱数の発生方法に問題があったと言う事です。(製作期間が数ヵ月程度では、デバッグ出来なかったのでしょうが…)
よくよく思い出してみると、このゲームには至る所でバランスの悪さがありました。例えば、戦闘中にやたらと攻撃をミスしたり、敵から逃げようとしてもなかなか逃げられなかったり等など。どれも乱数の発生方法に問題があったと考えれば非常に合点がいくものばかりです。
このゲーム、乱数バグがなければもっと高く評価されていたのではないでしょうか。
まあ、セガのゲームが好きな人達はおかしな人が多いので、多少ゲームのバランスが悪くても余裕でクリアしたりなんかしますが。
【まとめ】
・今はCPUに乱数発生回路が内蔵されている。M系列発生回路は想像つくが、CPU温度の小数点以下を乱数として使うなんてのもある。
・セーブするタイミングを間違えると、リセット攻撃が意味をなさいので注意。
・ゲーム機の内部変数が見えるようになると、某超能力ゲームも楽勝!
・頭に来たからといって、電源が入ったままカセットをぶち抜いて窓から投げだしたりしない。